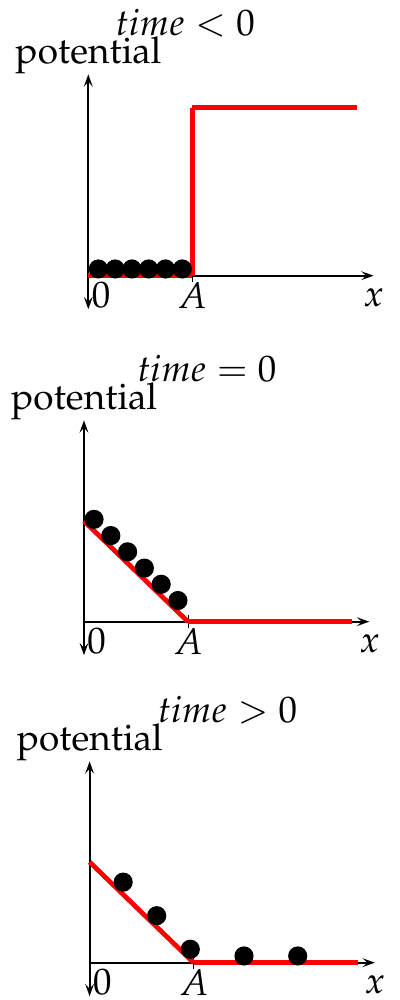
The fundamental question inspiring this project was how initially confined quantum mechanical particles relax towards a spatially extended region. To this end we studied a hypothetical experiment, first trapping a number of such particles in a box cut off from the remainder of a large system and then observing the dynamics when freeing them in a sudden quench.
Numerically simulating the depicted sudden quench protocol I analyzed features of the unitary relaxation of Bose-Einstein Condensates towards a spatially extended region for various forms of potentials. This lead to surprising and unintuitive effects. For instance, the expulsion from the energetically unfavorable region is only possible up to a specific threshold for the steepness of the potential. For slopes that are higher than this threshold the trapped particles oscillate.
To understand the dynamical trapping I then developed an analytical semi-classical model allowing a very good understanding and prediction of the trapping and also of the oscillations.
These results were published alongside other results from DMRG simulations done in my research group in a publication in Phys Rev A 86 (2012).
The hypothetical experiment is shown in the picture above. Starting from a condensed thermal ground state we expel particles by tilting the underlying potential. In the figure, the tilting is exemplary shown as a linear ramp but can be any kind of repelling potential shape. From a classical point of view we expect the particles to slide down this ramp (as depicted in the figure on the right) and diffuse into the remaining system colliding or interacting otherwise with each other.
However, in our case these particles are bosons at very low temperatures (Bose-Einstein-Condensates) and hopping from site to site on a chain of only some possible discrete positions. This scenario has applications in the study of quantum computing or the linking of atomic orbits to a large bulk material. Furthermore it has the advantage to be reproducible by recent experiments of trapping dipolar atoms in periodic laser fields allowing to fine-tune all involved parameters.
The boson character of the particle density we study on this chain makes the application of quantum field theory, i.e. the Bose-Hubbard Model, and some simplifications necessary. On one hand we assumed the system to conserve energy due to the short relaxation timescales thus generating the unitary character of the dynamics. Furthermore we placed ourselves in the low-temperature limit of the dynamics, thereby reducing the number of possible particles on a lattice site to be one or zero and thus to hard-sphere exclusion on each site. Using those simplifications we performed a Jordan-Wigner-Transformation to a fermionic system and then studied different initial particle densities, quench potentials (most prominently the linear ramp and the step-potential) and their implications on the dynamics as well as finite size effects.
In preliminary studies we found that in contrast to a classical system of particles the bounded kinetic energy has a surprising effect on the departure dynamics. Notably, a steepening of the evicting potential only results in an increase of the diffusion of the particles up to a certain steepness threshold depending on the initial particle density and the form of the potential. An evicting potential higher than this critical value results in particles being trapped inside the non-flat (initial) region. This effect was quantified analytically for various potential shapes and shown to be a direct consequence of energy conservation in the system.
To understand the dynamics of the evicted and trapped particle density observed in the simulations we developed a fluid-like semi-classical model for an analytical description of his system.
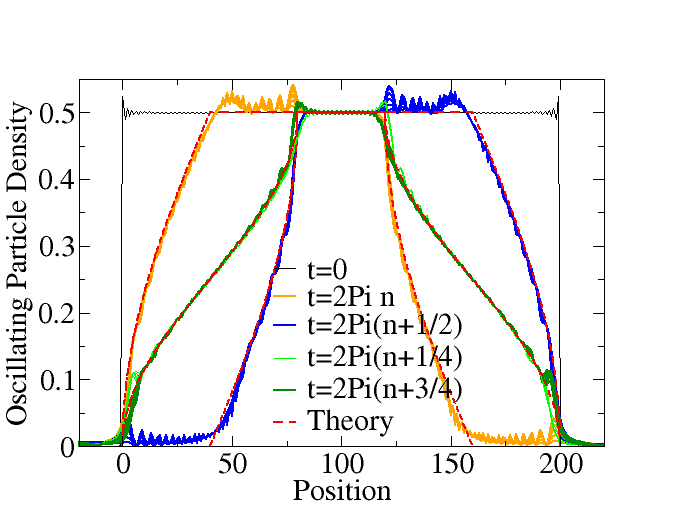
Using this model our primary focus then shifted towards the features of the dynamics of the particles trapped inside the region of the repelling potential. Most prominently inside the region of a linear ramp we made the observation of particles moving back and forth between two spatial areas inside the trapping region, which can be interpreted as oscillations between two macroscopic states.
This behaviour is shown in the figure, where multiple curves that differ by exactly one period of the oscillations overlap.
The trapped particle oscillation between these two regions could analytically be characterized through our semi-classical approach characterizing their frequency, form and spatial borders up to finite size effects observed numerically. In addition to the understanding we gained for this effect it may in applications be exploited as mechanism to increase the particle density by cutting off the sites of one of the two states at the right moment condensing all the oscillating particles in the other.
If you would like more detail, you can download a copy of my thesis here.
